
Содержание:
Что такое фрактал
Фрактал — это математическая структура, которая характеризуется самоподобием. Так называются схожие элементы, повторяющиеся на разных масштабах. Это понятие появилось в математике благодаря французскому математику Бенуа Мандельброту [1]. В 1975 году он образовал этот термин от латинского слова fractus — «дробленый» или «раздробленный».
Фракталы стали популярны благодаря своему применению в математике, компьютерной графике, различных природных и социальных явлениях. Они позволяют моделировать сложные структуры, которые иначе было бы трудно описать, такие как формы гор, облаков или деревьев.
Элементы фракталов подчиняются простым математическим правилам, создавая сложные структуры с помощью повторения и масштабирования. Из-за этих свойств они обладают бесконечным количеством деталей, которые можно разглядывать под разными уровнями увеличения.
Виды фракталов
Фракталы можно разделить на несколько основных типов в зависимости от их математических свойств и метода построения.
Геометрический

Эти фракталы основаны на геометрических правилах, которые применяются к простым формам для создания более сложных структур [2]. Яркий пример — это снежинка Коха, в рамках которой на сторонах правильного треугольника появляется замкнутая кривая бесконечной длины. Геометрические фракталы обладают высокой степенью симметрии и легко визуализируются благодаря своей структурированной форме.
Алгебраический

Алгебраические фракталы создаются с помощью математических формул, которые применяются к координатам точек [3]. Они строятся на основе повторения функции комплексных чисел. Их форма бесконечно усложняется при увеличении масштаба. Алгебраические фракталы часто используются для визуализации сложных чисел и моделирования динамических систем.
Стохастический
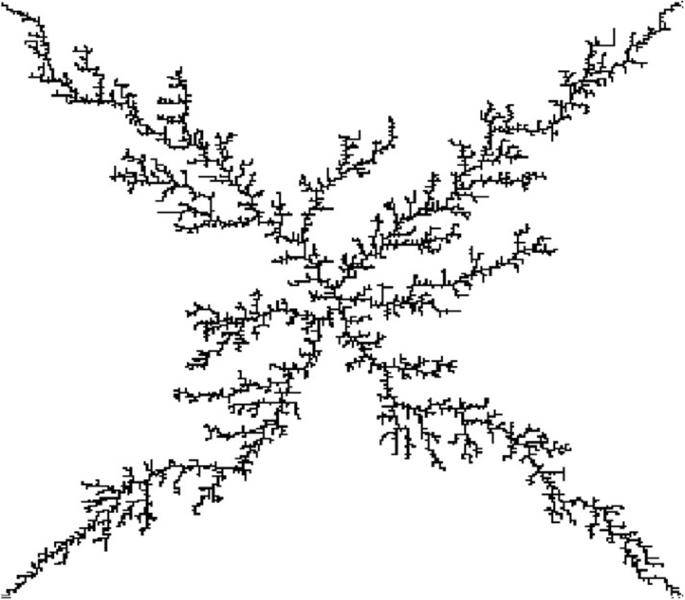
Стохастические фракталы (от греческого слова στοχαστικός — «предполагать», «угадывать») отличаются тем, что включают в себя случайные элементы [4]. Они имитируют объекты, которые невозможно описать строгими математическими правилами, например, форму береговой линии или поверхность гор. Стохастические фракталы применяются в моделировании природных явлений, где присутствуют случайные процессы.
Примеры фракталов
Количество фракталов бесконечно. Однако существует несколько самых известных, каждый из которых обладает уникальными свойствами и историей создания.
Множество Мандельброта
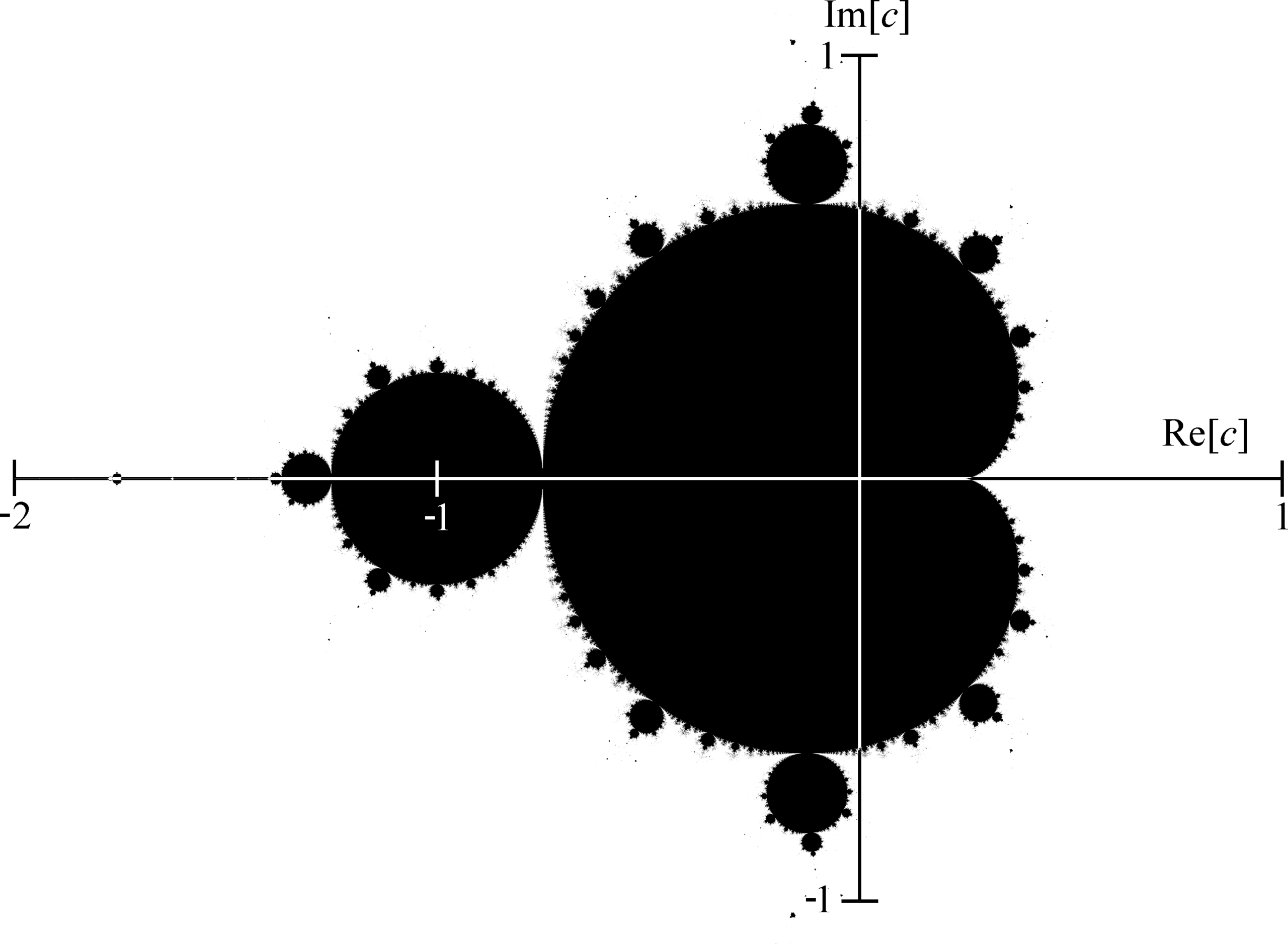
Множество Мандельброта — один из самых известных фракталов, который был впервые описан в начале ХХ века французским математиком Пьером Фату. Однако он физически не мог сформировать изображение, так как требовалось гигантское количество вычислений. Визуализировать множество с помощью компьютера удалось математику Бенуа Мандельброту в марте 1980 года [5].
Этот фрактал строится на основе простой функции комплексных чисел и создает сложную структуру с бесконечным числом деталей. Он используется в математике и визуализации для демонстрации самоподобия и исследуется как пример нелинейной динамики.
Канторово множество
Канторово множество — это простейший фрактал, представляющий собой отрезок, который делится на три части, при этом средняя удаляется [6]. Бесконечное количество раз формируется множество точек, которые не касаются друг друга, но остаются в одной прямой линии. Множество Кантора используется для понимания теоретических аспектов самоподобия.
Снежинка Коха
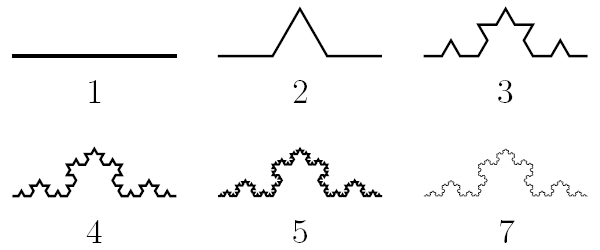
Снежинка Коха — фрактал, созданный шведским математиком Хельге фон Кохом в начале XX века. Специалисты портала «Элементы большой науки» отмечают: «Она получается из трех копий кривой Коха. Эта кривая была придумана как пример непрерывной линии, к которой нельзя провести касательную ни в одной точке» [7]. Этот фрактал используется в математике для исследования понятий бесконечности и самоподобия.
Треугольник Серпинского
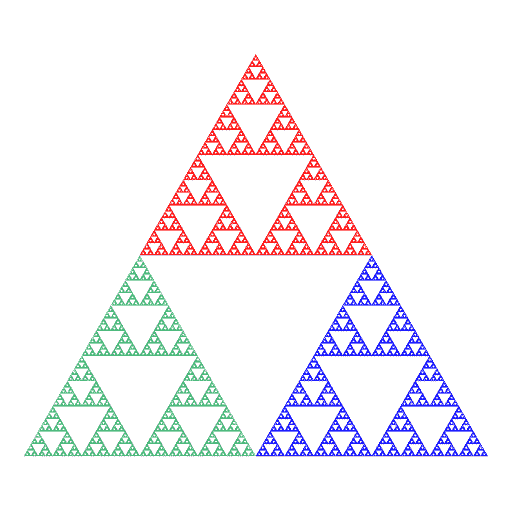
Треугольник Серпинского был изобретен польским математиком Вацлавом Серпинским в 1910-х. Он создается через деление равностороннего треугольника на четыре меньших, после чего центральный удаляется [8]. Этот процесс повторяется до бесконечности. Фрактал изучается в математике как пример самоподобия и фрактальной размерности.
Фрактал «Горящий корабль»
Горящий корабль — это менее известный, но визуально интересный фрактал, созданный как результат применения математических правил, аналогичных множеству Мандельброта. Визуально он напоминает разрушенное судно [9].
Фракталы в природе
Фракталы можно найти в самых разнообразных природных формах [10]. Например, такие свойства есть у листьев папоротника, деревьев и облаков. Они обладают способностью к самоподобию, что позволяет им развиваться по схожим правилам независимо от масштаба. Такая геометрия позволяет более эффективно использовать ресурсы и площадь, что играет ключевую роль в процессах роста и размножения.
Фрактал в капусте Романеско

Капуста Романеско — яркий пример природного фрактала. Ее бутоны напоминают спирали [11]. Каждая из спиралей состоит из мелких элементов, повторяющих форму более крупных. Структура помогает растению оптимально использовать солнечный свет и равномерно распределять питательные вещества.
Фрактал в математике
Фракталы играют важную роль в математике, особенно в изучении нелинейных систем и хаотических процессов. Они используются в анализе динамических систем и чисел, моделировании природных явлений, в том числе метеорологических процессов и турбулентных потоков. Алгебраические фракталы, такие как множество Мандельброта, позволяют ученым исследовать сложные математические модели и развивать новые подходы к изучению самоподобия и бесконечности.
Фракталы также используются для создания компьютерной графики, визуализации данных и даже в развитии искусственного интеллекта. Их свойства помогают находить оптимальные алгоритмы для обработки изображений и создают визуально привлекательные композиции.
👀 Следите за телеграм-каналом «РБК Трендов» — будьте в курсе последних тенденций в науке, бизнесе, обществе и технологиях.







