Что такое числа Фибоначчи
Числа Фибоначчи — это математическая последовательность, в которой каждое последующее число равно сумме двух предыдущих. Начинается последовательность с нуля и единицы или с двух единиц — в зависимости от выбранной формы записи. Если взять базовый вариант последовательности, начинающийся с 0 и 1, то первые несколько чисел выглядят так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,...
Где:
- 0 и 1 — первые члены последовательности;
- 1 = 0 + 1;
- 2 = 1 + 1;
- 3 = 1 + 2;
- 5 = 2 + 3;
- 8 = 3 + 5;
- и так далее.
Феномен последовательности не только в ее простоте, но и в том, что она удивительно часто встречается в самых разных аспектах нашей жизни: от формы ананаса, очертаний ураганов и звездного неба до логотипа Apple или постеров фильма «Звездные войны»[1].
История чисел Фибоначчи
Впервые этот числовой ряд описал в 1202 году итальянский математик Леонардо из Пизы. Позже он стал известен как Фибоначчи. Прозвище означает «сын Боначчи» и указывает на его семейное происхождение.
Отец Леонардо был купцом и часто брал сына с собой в далекие страны. Во время таких поездок юный Леонардо обучался математике у арабских учителей, которые считались лучшими специалистами в этой науке [2].
Арабские переводы познакомили его с математическими трудами античных и индийских мыслителей, что значительно расширило его кругозор. Все свои открытия Фибоначчи позже описал в «Книге абака» (Liber Abaci) [3], где показал, насколько удобны арабские цифры, и предложил любопытные задачи — среди них прославленная задачка про кроликов.
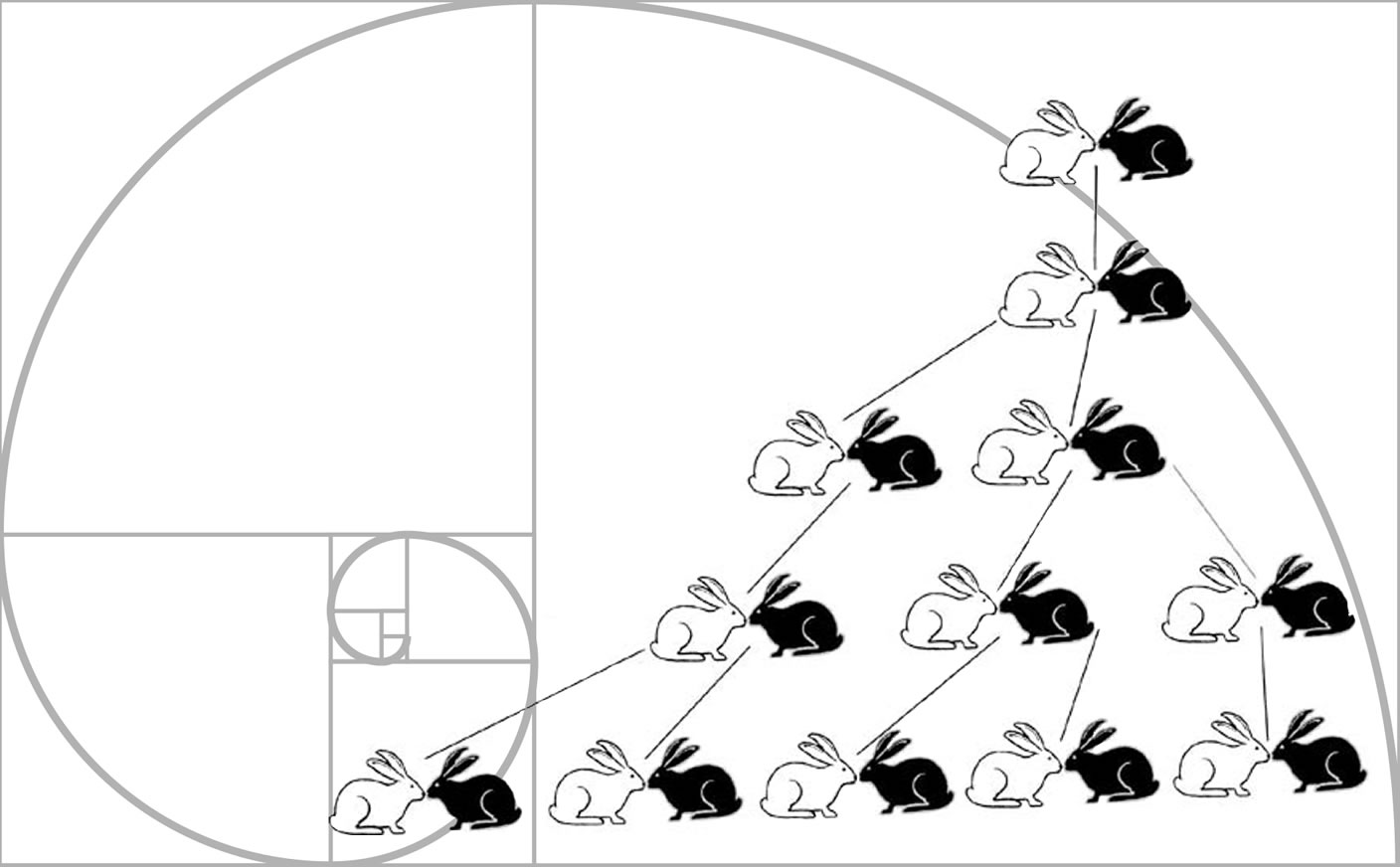
Вот как сформулирована задача: «Представим, что у нас есть пара новорожденных кроликов (самец и самка). Спустя месяц они приносят первое потомство — новую пару, и теперь у нас уже две пары. Каждый новый кроличий «подросток» тоже начинает размножаться через месяц. Сколько всего пар кроликов будет через x месяцев?»
Если последовательно решать эту задачу, то у вас получится та самая последовательность Фибоначчи. Вот пример такого решения [4]:
- Месяц 0: 1 пара (новорожденные).
- Месяц 1: все еще 1 пара (просто подросли, еще не размножались).
- Месяц 2: появляется первая новая пара → 2 пары.
- Месяц 3: первая пара снова приносит потомство → 3 пары.
- Месяц 4: потомство от обеих «взрослых» пар → 5 пар.
... и так далее.
У Леонардо Пизанского есть и другие математические заслуги, помимо открытия чисел Фибоначчи. Он ввел понятия «плюс» и «минус», правда обозначал ими ошибки в вычислениях: когда результат получился больше или меньше правильного.
Формула чисел Фибоначчи
Последовательность Фибоначчи можно выразить несколькими формулами. Наиболее известная — рекурсивная [5] и выглядит вот так:
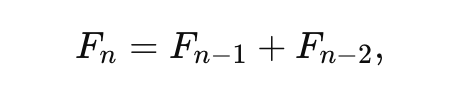
С ее помощью легко понять принцип образования каждого нового члена последовательности, но сама рекурсия порой неудобна при больших вычислениях, так как требует повторного вычисления предыдущих значений.
Для упрощения вычислений придумана формула Бине [6].
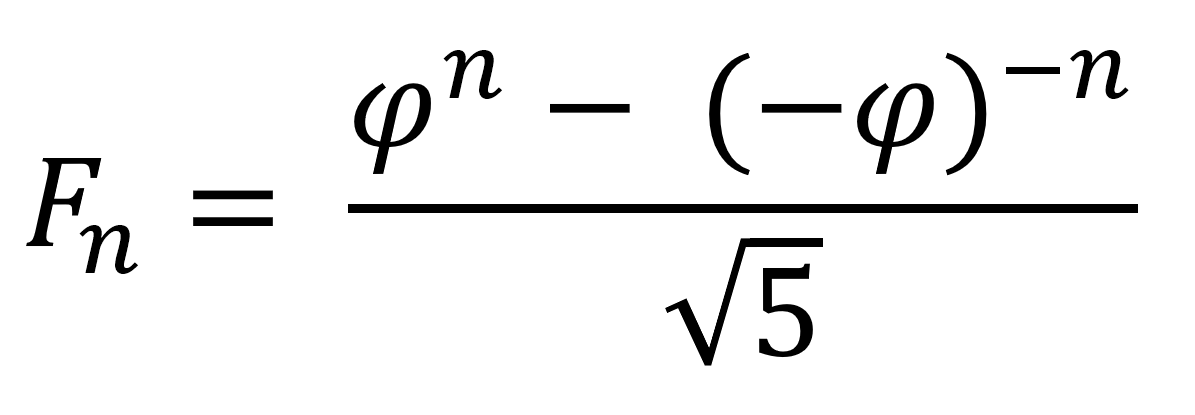
К сожалению, эта формула не всегда подходит для точного вычисления чисел Фибоначчи на практике. Проблема в том, что число Фидия (φ), известное как золотое сечение, примерно равно 1,618 и является иррациональным. Если мы рассчитываем значения напрямую по формуле, существует риск накопления ошибок из-за округлений. Чтобы убедиться в точности итоговых чисел, придется проводить дополнительные проверки, если мы говорим об очень больших значениях. Проще говоря, золотое сечение — это геометрическое отражение связей между соседними числами в ряду Фибоначчи или идеальная пропорция, приятная для взгляда и удобная для работы.
Числа Фибоначчи и золотое сечение
Спираль Фибоначчи — это узор, построенный на основе последовательности одноименных чисел. Он создается так:
- Рисуем серию квадратов, у которых длины сторон соответствуют числам Фибоначчи (1, 1, 2, 3, 5, 8 и т.д.).
- Начинаем с маленького квадрата, затем рядом добавляем квадрат чуть больше, и так каждый раз: новый квадрат получается размером, равным сумме длин сторон двух предыдущих квадратов.
- Внутри каждого квадрата проводим четверть окружности (дугу), которая «переходит» в следующий квадрат, формируя спираль. Она будет бесконечно расширяться, и чем дальше мы ее продолжаем, тем ближе этот рисунок будет к золотому сечению.

Художники, архитекторы, дизайнеры, фотографы и поэты применяют это соотношение, чтобы придать своим работам «правильные» и гармоничные пропорции, которые может заметить даже нетренированный глаз человека.

Где можно встретить и использовать числа Фибоначчи
Область применения или возникновения чисел Фибоначчи столь широка, что они то и дело появляются порой даже в самых неожиданных местах.
Вот несколько сфер, где их можно встретить и, конечно же, применять:
В природе
- Распределение семян подсолнечника: зернышки образуют спирали, количество которых по часовой и против часовой стрелке часто соответствует соседним числам Фибоначчи [7].
- Шишки и ананасы: наглядно на них можно заметить характерные узоры — спиралевидные ряды, количество которых равняется двум соседним членам последовательности [8].
- Лепестки цветов: у многих видов растений число лепестков соответствует одному из чисел Фибоначчи (3, 5, 8, 13 и т. д.).

Ученые считают, что такая «упаковка» помогает растениям размещать листья или семена для эффективного использования пространства для роста. Некоторые исследования показывают, что расположение листьев по принципу Фибоначчи не обязательно дает растению решающее преимущество в поглощении солнечной энергии [9]. Оказалось, что и другие, похожие на Фибоначчи схемы могут быть столь же эффективны с точки зрения фотосинтеза. Значит, для эволюции все подобные варианты могут оказаться примерно равными, а если у размещения по Фибоначчи и есть особая польза, то она, скорее всего, не связана напрямую с поглощением света.
В дизайне
Дизайнеры и архитекторы часто стремятся к «гармоничному» построению форм. И здесь на помощь приходит золотое сечение, тесно связанное с числами Фибоначчи. Именно поэтому:
- Логотипы часто создаются из прямоугольных элементов, стороны которых соответствуют последовательности Фибоначчи. Это придает итоговому изображению узнаваемый и стройный вид.
 Логотип социальной сети Twitter (ныне X)
Логотип социальной сети Twitter (ныне X) - Типографика: при выборе идеальных отступов, размеров шрифта и структуры макета иногда используют числа 8, 13, 21, 34 и т.д., чтобы добиться балансировки пространства.
В архитектуре и искусстве
Многие известные здания — от античных храмов до современных музеев — проектировали, опираясь на пропорции, максимально приближенные к золотому сечению, а значит, связанные и с рядом Фибоначчи. Особенно часто эту гармонию прослеживают в шедеврах эпохи Возрождения и стиля барокко.
Не только архитектура, но и живопись дает примеры «золотых» закономерностей. В одном исследовании ученые рассмотрели работы 200 знаменитых художников (в том числе Пабло Пикассо, Клода Моне и Франсиско Гойи) и выяснили, что лучшие произведения они создавали примерно в возрасте 42 лет [10].
Это значение оказалось чуть меньше двух третей средней продолжительности их жизни — примерно 0,6198. Оно почти совпадает с легендарной пропорцией золотого сечения.

В программировании и IT
В сфере программирования и IT задача на вычисление чисел Фибоначчи считается своеобразной «проверкой на джуна»[11]. Ее часто дают новичкам, чтобы проверить базовые знания алгоритмов и убедиться, что кандидат умеет писать корректный код. По сути, это простой пример рекуррентной функции, который отлично показывает, как разработчик подходит к построению и оптимизации алгоритмов.
Помимо этого, последовательность Фибоначчи нередко используется в Agile-подходе[12]. Там она помогает оценивать сложность задач во время так называемых «покер-сессий». Каждый член команды получает набор карт, соответствующих ряду Фибоначчи, и, когда наступает черед оценить задачу, все одновременно показывают карту с номером, отражающим их оценку.
После этого участники обсуждают, почему выбрали тот или иной балл, и стараются прийти к общей цифре. Такой метод избавляет от путаницы при ручном суммировании или выведении среднего, а главное — помогает всей команде взглянуть на задачу с разных сторон.
В финансах и трейдинге
Мир финансов, будучи тесно связанным с цифрами, также оказался очарован последовательностью Фибонначи.
Часто трейдеры и аналитики [13] применяют уровни Фибоначчи, чтобы понять, где цена может развернуться, сделать откат или продолжить движение вверх или вниз. Для такого прогнозирования движения цены они ориентируются на уровни поддержки и сопротивления. Поддержка — это ценовой уровень, ниже которого сложно опуститься. Сопротивление — уровень, при приближении к которому цена обычно останавливается или разворачивается вниз. Уровни Фибоначчи выступают одним из инструментов, которые трейдеры применяют для определения этих уровней. Для этого они создают на графике ценообразования так называемую сетку Фибонначи, где, например, на уровне 618 [14], становится видно, где цена может отскочить обратно после падения или повышения.
Метод популярен в том числе и среди новичков на фондовом рынке, благодаря своей универсальности — он одинаково хорошо работает для разных активов и на любых временных отрезках. Такой график легко построить, нужно лишь задать несколько коэффициентов и выбрать две характерные точки, а также его можно совмещать его с другими инструментами.
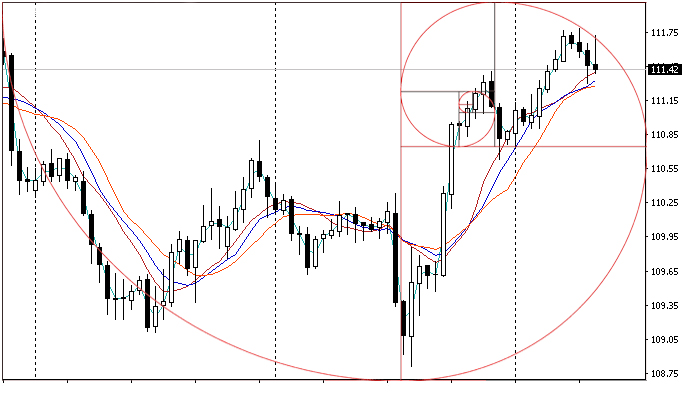
Важно подчеркнуть, что реальной связи между уровнями Фибоначчи и поведением цен на рынках нет. Уровни Фибоначчи рассчитываются исключительно на основании исторических графиков торговли активами, при этом не учитываются важные фундаментальные факторы, такие как финансовые отчеты компаний или последние новости. Поэтому использовать лишь этот метод для принятия инвестиционных решений недостаточно [15].
В мемах и юморе
Последовательность Фибоначчи и золотое сечение успели войти и в интернет-культуру. Пользователи любят шутить, обыгрывая «идеальную пропорцию» и контраст между совершенством и чем-то далеким от него.
Есть и примеры каламбуров: «Каждая новая шутка про Фибоначчи смешнее двух предыдущих вместе взятых!» Можно предположить, что через мемы и юмор многие параллельно запоминают сам принцип построения легендарного ряда.
Читайте также:
➤ Подписывайтесь на телеграм-канал «РБК Трендов» — будьте в курсе последних тенденций в науке, бизнесе, обществе и технологиях.










